Dreaming, Vol. 3, No. 3, 1993
Self-Organization Theory of Dreaming
David Kahn1 and J. Allan Hobson l,2
Our general hypothesis is that the brain self-organizes neuronal signals whose cognitive correlates produce discontinuities and incongruities in an on-going narrative. This could go on in any sleep-wake state but, according to our theory, it is qualitatively distinctive in REM sleep/dreaming. To demonstrate the origins of this idea, we review the cognitive psychology of dreaming and the neurophysiology of rapid eye movement sleep in terms of the self-organization concept. We also review mathematical models of self-organization for their relevance to dreaming. We then go on to test our hypothesis in a preliminary way at the level of neurophysiology. Bifurcation parameters were chosen to be the relative amounts of cholinergic and aminergic neurotransmitters, the burst frequency of pontogeniculoocipital (PGO) waves (producing noise-induced transitions), and an electrical activation parameter. A class of mathematical models universally applicable to self-organizing systems near the system’s bifurcation points was found to model the neurophysiology in a formal manner isomorphic to distinctive and global cognitive features of dreaming.
KEY WORDS: self-organization; REM; dreaming; bizarreness; PGO bursts.
The goal of this paper is to examine the thesis that the dreaming brain is a self-organizing system. The essence of the concept of self-organization is that ordered interactions between elements in a complex system may form without any higher control when the system is driven away from equilibrium. A constraint such as a change in the relative amounts of two or more neuromodulatory influences may drive a neural network from equilibrium. If the constraint is large enough, a critical value may be reached whereby the network self-organizes, that is, it forms a pattern which did not exist before. Thus, when the brain undergoes a change in state, say from non REM to REM sleep, it may self-organize in a radically new way. Since we assume that our conscious experience is a function of its underlying brain state we can expect the cognitive features of dreaming to reveal the normal self-organization properties of the REM sleep brain.1
Aspects of self-organization have been examined in the waking brain by, among others, Atlan (1987, 1989), Antrobus (1991), Babloyantz et al (1985), Clark et al. (1985), Erdi & Barna (1987,1984), Edelman (1990), Gray et al. (1989), Singer (1989a, 1989b, 1988), Sutton et al. (1988), and Szentagothai & Erdi (1989). And a few papers have presaged self-organization phenomena in the dreaming brain, e.g., Antrobus (1991), Globus (1989), and especially the paper by Mamelak and Hobson (Mamelak & Hobson, 1989b), which introduced ideas that foreshadow the theory of self organization of dreaming suggested here and in Kahn & Hobson (1991a, 1991b).
NEUROPHYSIOLOGICAL AND COGNITIVE CORRELATES OF DREAMING
The first dream theory to be based upon specific neurobiological findings was the activation synthesis hypothesis of Hobson and McCarley (1977) which attributed the peculiar aspects of dream consciousness to the forebrain's attempt to integrate chaotic signals arising in the brain stem. In order to correlate specific cognitive facets of dreaming with neurophysiological conditions more precisely, the revised activation synthesis model of Mamelak and Hobson (1989b), theorized that aminergic demodulation of the brain increased the probability of spontaneous neuronal firing in the forebrain. This in turn led to an unpredictability or infidelity of neuronal activation, which, in turn, produced such cognitive defects as discontinuities and incongruities in narrative which constitute dream bizarreness (Hobson, et al. 1987).
The Putative Uniqueness of Dream Bizarreness
Before proceeding to further discussion of how REM sleep neurophysiology might contribute to such dream features as discontinuity and incongruity, it is important to clarify our position regarding the putative uniqueness of such cognitive features to dreaming. Let us first formally acknowledge that the empirical evidence for the cognitive uniqueness of dreaming is contradictory, controversial, and— to most researchers—unconvincing. In other words, the results of most studies of dream-like mentation suggest that all of its qualities can be found in reports of conscious experience in waking and non REM as well as REM sleep [see, for example, Moffitt et al. (1982)].
We recognize both the validity of these empirical findings and their implication: that there is some continuous function, such as the general level of activation, which determines the robust quantitative differences in dreaminess that distinguish the states. But we would like to enter two important caveats of great relevance to any dream theory and of particular relevance to our self-organization hypothesis. The first caveat is that there is, already, undeniable evidence of the qualitative distinctiveness of dreaming in the bizarreness subcategory of character discontinuity and incongruity. Thus we know of no claim that the persons imagined by us in normal waking undergo character transformation either by transmogrification (as in the changes in the Portrait of Dorian Gray) or by the condensation of two persons (or two sexes) into a single character. The second caveat is that, as dreamers, we ourselves experience states of consciousness in dreaming which seem to us to be qualitatively different from waking. Two examples will suffice: one is the loss of self-reflective awareness that Sartre correctly underlined as distinctive of dreaming (Sartre 1980); another is our almost complete inability to direct either our thoughts or our actions in dreaming (Hartmann 1973). Because these are both negative features of dreaming no one has, as yet, assiduously tried to measure them.
With respect, we therefore urge our skeptical colleagues to keep an open mind on the issue of the uniqueness of dream cognition. If there is already evidence of some such properties, we suggest that affirmative probes, such as those we have used to explore dream emotion (Merritt et al. 1993), and dream bizarreness in children (Resnick et al. 1993), will find more. And, as we will see, the self-organization model suggests that we should be able to find mental state features distinctive of dreaming.
Neuronal Demodulation and Dream Bizarreness
The Mamelak-Hobson update of the activation-synthesis hypothesis used a probabilistic activation function to model a demodulated neuron which has a certain probability of firing. When this demodulated neuron is a part of a network, many possible output patterns can be generated with even one input, owing to the unpredictable nature of the neuronal response. Neurons just below firing threshold may in fact fire, and those just above may not fire depending on the quantitative level of uncertainty in neuronal firing.
But it is also known that combined with the withdrawal of aminergic inhibition there is a reciprocal cholinergic excitation. In dreaming, neuronal activation patterns are discontinuously switched as a result of phasic bursts of acetylcholine (Ach) activating otherwise quiescent neurons. According to the theory, this switching in neuronal firing patterns has its cognitive correlate in the discontinuous jumps between dream events. The theory of Mamelak and Hobson postulates that the cholinergic pontogeniculoocipital (PGO) system is responsible for discontinuous jumps in dream narratives.
SELF-ORGANIZATION HYPOTHESIS OF DREAMING
We now further postulate that a disinhibited forebrain not only produces neural network errors, but is driven far from equilibrium especially when also subject to strong phasic cholinergic input. The strong phasic cholinergic input, in the form of PGO bursts, gives rise to self-organized processes. The individual PGO-induced self-organized processes are identified cognitively with dream images, while the overall structure is the dream plot or the overall self-organization of the dreaming brain.
A dream image may be defined as any unit of self-generated conscious experience in the domains of perception, cognition, or emotion. As a rule the dream images that arise in these three domains are integrated, or at least interrelated and contained within a narrative/scenario framework such that our conscious experience of them is unified.
The resultant dream narrative is the joint product of a top-down cognitive process which incorporates the randomly generated bottom-up images which produce incoherences in the on-going dream plot (Hobson, 1988; see also Posner, 1989). Thus dreams have two complementary aspects: they have a coherence or unifying theme that generally runs throughout at least long segments of the dream (see Stickgold, et al. 1993b), and yet they also contain incoherences or marked digressions from the main theme. In any dream theory this apparent paradox must be addressed.
We speculate that coherent aspects of dreaming are present when self-organization is working optimally (as occurs in the waking brain), while incoherent or bizarre aspects reflect the failure of the brain-mind system to organize all features of the signals it internally generates into a consistent narrative. This results when PGO-induced self-organized neural processes remain as separately created structures from the overall neural self-organization that is occurring. Bizarre aspects of dreaming occur when there is an incongruous incorporation of these PGO-induced neural patterns into the overall neural pattern. The cognitive correlates of the PGO induced self-organized patterns are randomly occurring dream images.
To illustrate the interaction between the coherent macrostructures and incoherent microstructures in dreams, we have reexamined the "Customs House" dream, one of many from the journal of the so-called Engine Man, originally analyzed in Hobson (1988) and cited, in full, in Mamelak & Hobson (1989b). Here we present a representative journal passage as Figure 1.
There is a clear macrostructure to the Customs House dream; a narrative exists, bizarre though it may be, and narrative coherence is established by two themes one of nurturance and the other of authority (Hobson, 1988). These themes are cast in the dream within the framework of searching. First there is the looking for a building called the Customs Building. Within the building the process of searching continues with the Engine Man looking for the right part of the building to be in and with his looking into several different rooms.
However, in the process of these searches, different microstructural elements incongruously appear such as the image of "ramps on outside apparently to enable animals to reach the upper stories. . ." One would not expect the Customs House to house animals nor to contain ramps. Other incongruous images that make their way into the narrative include ". . a large, cradle-like bed in which were a fully dressed nurse, and a baby." In another room there are young children with ancient faces, and in another a judge and the author's two sisters. Although they may have a deeper associative relevance, these and other microstructural elements of the dream are woven into the narrative in only a superficially logical and partially consistent way. In a sense they therefore remain as separately created structures that are only incongruously tied to the on-going narrative. We shall have other occasions to refer, and to cite specific passages from this dream as we develop the theory further.

Fig. 1. Page From Customs House Dream. Photographic reproduction of a page in a dream journal giving a narrative and a pictorial account of a dream about a customs building which the dreamer and his nephew seek, and find, in downtown Washington. [Reproduced with permission from Hobson, et al. 1987].
_______
REVIEW OF THE NEUROPHYSIOLOGY OF REM SLEEP
The state of the brain depends upon the level of excitation and inhibition in its constituent neural networks. Of these, critical neuronal populations of chemically specific cells are found in the pontine brain stem. These populations include the noradrenergic locus coeruleus (LC), the Serotonergic Dorsal raphe nucleus (DRN), and the cholinergic pedunculopontine nucleus (Hobson, 1990a).
It must be noted that the action of the neuromodulatory systems on neuronal excitability and inhibition is very complex involving a number of neurotransmitter systems, including the dopamine system, which we neglect in this review. Thus, the restriction of our attention to the noradrenergic, serotoninergic, and cholinergic systems provides an incomplete description of the brain's modulatory systems. However, we feel justified in restricting our study to these neurotransmitter systems because previous studies have shown the unique importance of these systems to the neurophysiology of dreaming. If and when other modulatory brain systems are sufficiently experimentally implicated in dreaming, we would include these in our theoretical formulation and thereby obtain a more complete description of the complex modulatory systems of the brain.
LC neurons use norepinephrine (NE) as a neurotransmitter and neuromodulator which acts hormonally in the sense that it biases the brain toward specific state-like behavior, e.g., waking. As a neurotransmitter it acts by increasing or decreasing the spontaneous firing of other neuronal ensembles so as to increase the signal to noise ratio and thereby enhance attention (Sutton, et al. 1992; Keeler, et al., 1989, Servan-Schreiber, et al. 1990). As a neuromodulator it acts post synaptically via the second messenger CAMP, and thus may influence attentional mechanisms, and information processing, e.g., memory, and learning (Flicker, et al. 1981, Mamelak & Hobson, 1989b).
There is a similar serotonergic system and its neurons are in the mid line of the brain stem in a set of nuclei called the raphe. Serotonin is an inhibitory neurotransmitter with neuromodulatory actions also mediated by cyclic AMP (Hobson & Steriade 1986, Hobson & Schmajuk, 1988, Flicker, et al. 1981). The functional role of serotonin in cognition is less clear but it has been proposed to mediate behavioral inhibition, perhaps by holding motor pattern generators just below threshold so that a vast repertoire of behaviors is readily available for selective activation by the appropriate signal. This concept is the output side equivalent of selective attention which gates inputs.
The NE and 5HT neurons have leaky membranes and act like pacemakers constantly firing during the wake state at a rate of two to four spikes per second bathing the cortex with NE and 5HT. It is this tonic firing that may serve to keep us awake. The brain changes state from waking to sleep when these pacemaker neurons are damped producing less NE and 5HT. During the REM period they cease firing altogether (Hobson & Steriade 1986, Hobson, 1989b, Hobson & McCarley, 1977). The mechanism by which LC and DRN activity is arrested in REM sleep is unknown but some investigators have suggested a direct inhibitory effect from the reticular formation (Aghajanian & Van der Maelen 1986; Sakai, et al. 1977).
PGO Waves and the REM Generator
As the activity of aminergic pontine reticular formation neurons from the LC and the DRN declines, the excitability of cells that they inhibit increases. These REM-on cells, which are found in several brain stem nuclei contribute a putative REM sleep generator population. Among the systems that are disinhibited are the pontine reticular formation neurons themselves. One particularly interesting group of REM-on cells are the so-called "PGO burst" cells in the cholinergic pedunculopontine nucleus (CH6). These pontine formation neurons fire single spikes during waking (when they are assumed to enhance sensorimotor integration, Callaway, et al. 1988) but discharge in clusters in REM sleep (Hobson, 1990a, Hobson & McCarley, 1977, Quattrochi, et al. 1989).
There is evidence that PGO activity is correlated with increased firing in the visual cortex and in the lateral geniculate bodies (LGB) (Callaway, et al. 1988; Singer, 1989b). Increased PGO activity in the visual cortex could, therefore, lead to more dream images being formed by causing neuronal networks in the visual cortex to reach the threshold frequency necessary for image formation.
There is also strong evidence that complex motor patterns are commanded at the level of the brain stem but blocked at the level of the spinal cord, so that the only outward sign are the REMs themselves and small muscle twitches. Since the PGO-related neuronal firing encodes some aspects of these motor commands, it is possible that the forebrain incorporates information about this fictive movement into the dream (for a complete discussion of this concept see Porte & Hobson, 1993). We freely acknowledge that our ideas on the phenomenology and psychophysiology of dreaming are not universally accepted and the reader interested in an intelligent discussion of one strongly dissenting view is referred to Antrobus, 1991.
RECENT STUDIES OF DREAM PSYCHOLOGY WITH SPECIAL
REFERENCE TO SELF-ORGANIZATION
The nature of dream bizarreness and its difference from waking mentation has been investigated by McCarley and Hoffman (1981), Hobson, et al. (1987), Williams, et al. (1990, 1991), Rittenhouse, et al. (1993) and by Sutton, et al. (1993a and b). Bizarreness is defined as highly unlikely elements in the dream narrative. Such improbable events are usually associated with discontinuities of time, place, person, object and action as well as incongruities of these same features. Discontinuities include abrupt shifts in dream narrative, and interruptions in orientational stability. Incongruities include inappropriate matching of different characters, objects or scenes of the dream story line.
Since so much of our recent work in dreams has been done by analyzing reports gleaned from sleepers following spontaneous, home-based awakenings, we must comment on our assumption that most such reports are indeed reflections of the consciousness associated with REM and non REM, sleep. Utilizing our home-based sleep monitoring system, the Nightcap (Mamelak & Hobson, 1989a) we have recently been able to confirm the laboratory based assumption that 80% of reports exceeding 14 lines in length are, indeed, obtained following arousal from REM sleep (Stickgold, et al. 1993a).
All of these empirical studies, undertaken at our laboratory and elsewhere, support the notion that dream bizarreness is the result of a state-dependent cognitive process that has its roots in REM-sleep neurophysiological processes.
Williams, et al. (1990, 1991) conducted a quantitative study of bizarreness using home-based dream reports and daytime fantasies of twelve adult subjects. The subjects were asked to record all dreams remembered upon awakening in the morning. The subjects were also asked to indulge in fantasizing during the day and to record these fantasies as well. 120 dream and fantasy reports ~(sixty each) were collected from the twelve subjects, using only those subjects who were able to turn in ten dream reports and ten fantasy reports. The reports varied in length from 30 to 600 words.
The dream reports were found to be both quantitatively and qualitatively different from the waking fantasy reports. While bizarreness also occurred in waking fantasies, it did so significantly less often: dreams showed a two-fold greater bizarreness density (normalized for report length) than fantasy reports, and dreams were easily distinguished from fantasy reports in blind scorings (with 90% accuracy) based on the bizarreness measure. (See Rittenhouse, et al. (1991, 1993) for an indepth study of discontinuities that occur in dreams.) These new results are consonant with the present self-organization theory and with the activation- synthesis theory of dreaming.
Self-organization theory predicts that a qualitative change in cognition will occur in REM sleep because of the incorporation of bottom-up images whose intensity and frequency are assumed to increase during REM sleep. These images are generated when neural processes self-organize as a result of increased cholinergic and decreased aminergic input onto forebrain structures. Both theories predict a difference between REM sleep dreams and waking fantasies as due to the difference in neuronal activities and neuronal chemistry of the brain in the two different states. In particular, there is a depletion of the brain stem-supplied aminergic neurotransmitters and the occurrence of an internal stimulus source in the form of PGO bursts during the REM state.
In the waking brain which is connected with the external world, thought processes remain generally stable, not easily dominated by stray thoughts or images. The waking brain discards or integrates such stray thoughts into previously learned experiences becoming quite insensitive to the influence of such outliers. An exception may be the creative insight which often is the amplification of an almost imperceptible thought/image/feeling. Contrastingly, the demodulated and PGO-activated dreaming brain, cut off from the external world, is ultra sensitive to stray images and thoughts. It thus has the ability to jump from one class of images/thoughts to another; that is, to bifurcate to entirely new and probably unrelated images/ thoughts. It may amplify "stray" images and thoughts, leading to incongruous scene shifts, responsible for the bizarreness of the dream.
This relationship between bursts of PGO activity and dream mentation is also consistent with another empirical study (Stickgold, et al. 1991, 1993b), where it was found that plot shifts often result in profound plot disruption. In this study, judges were asked to distinguish between intact dream reports and spliced dream reports, which were constructed from two or more dreams. The spliced dreams were constructed by recombining randomly selected segments from the different dreams. The randomly selected segments were defined by major scene shifts so that the dreams were spliced at discontinuities. Observers were unable to distinguish intact dreams from spliced ones, even when spliced dreams contained segments of dreams from two different subjects. Whatever thematic consistency exists in dream reports apparently lies mainly within a dream segment and not between segments separated by a major plot shift type of discontinuity. This is precisely what is predicted by the self-organization theory of dreaming: non-continuous jumps in neuronal processes occur which lead to qualitative shifts in dream plot such that dream segments separated by discontinuities can be entirely unrelated to each other.
The self-organization theory of dreaming is also in agreement with a statedependent neural network model with temporal sequencing capabilities investigated in our laboratory by Sutton, et al. (1991). Networks, consisting of 50 binary state elements were constructed so that each one had interconnections embedding six stable memory configurations. Two modulatory effects were modeled. One represented tonic aminergic modulation, while the other simulated excitatory facilitation, representing the phasic cholinergic activity and PGO waves found during REM sleep. The model was run to simulate the waking, NREM, and REM sleep states, respectively. The model REM state produced novel sequence formation, similar to the kind of learning that occurs during self-organization. The results of this neural network modeling thus support the theory of dreaming as a self-organizing process, predicting that new sequences of neuronal events may emerge following a burst of PGO activity.
Our attribution of a role for PGO-like activity in the determination of dream bizarreness has been questioned on two grounds. One is the previously discussed issue of the uniqueness of the association of dream mentation to REM (Bonato, et al. 1991). The other is the issue of whether or not REM-sleep consciousness is more dream-like when phasic events, like the REMs themselves and the PGO waves that are linked to them, are intense. The empirical evidence bearing on this point is contradictory, controversial, and inconclusive but our recent study of recall following spontaneous arousal at home showed that dream-like mentation was correlated with those REM periods that had high levels of eye-movement activity and with REM-rich segments within those REM periods (Stickgold et al 1993a).
Why Introduce A Self-Organization Theory of Dreaming?
The next question that must be addressed is what dream features are better accounted for by the self-organization theory than by other theories of dream formation? Our paradoxical answer is that any and all coherent aspects of the dream must be attributed to the brain's capacity to self-organize. This is because external space-time information which is encoded in relatively orderly mental representations of nature during waking is absent during REM sleep. We maintain that no other theory has even tried to deal with this problem in terms of specific cellular mechanisms. To cite activation, primary visual excitation, or even secondary cognitive elaboration is to beg this question entirely. We acknowledge that all these processes may be at work in dreaming but none of them is any more than description unless further elaborated. This paper begins such an elaboration.
CONCEPT AND EXAMPLES OF SELF-ORGANIZATION
The emergence of structure or order among interacting elements of a system through self-organization has been hypothesized to occur in many complex systems (Haken, 1981, Nicolis and Prigogine 1977). These include the cooperative food foraging behavior of social insects (Deneubourg, et al. 1987a, b), limit cycle formation among simple cellular automata (Atlan, 1987), resonance interactions among elements of the visual cortex and the formation of ocular dominance columns (Singer, 1988, 1989a, 1989b, Szentagothai & Erdi, 1989), laser operation (Haken, 1975, 1981), tumor growth in the immune system (Lefever, 1980, Hiernaux, et al. 1987), urban evolution (Allen, 1982), and family system dynamics (Elkaim, et al. 1987). The goal of this paper is to show that the dreaming brain is also a self-organizing system.
To understand self-organization, it is helpful to define the thermodynamic state of a system. This state represents the continuation of near equilibrium behavior as the distance from equilibrium is increased. Self-organization is the transition from this reference state, the thermodynamic branch, to solutions of a new type. These new solutions are characterized by long range correlations which can be created when a system is far from equilibrium. The amplitude of these correlations increases as the distance from non-equilibrium increases. As an example of the amplification of fluctuations in a system that is subject to strong non-equilibrium constraints and which leads to self-organization is the well-known Benard instability (Nicolis & Prigogine, 1977). In this example a pan of water is heated from below. At weak temperature gradients heat initially passes from the bottom to the top by thermal conduction. If the heat is increased so as to increase the temperature difference between the top and bottom, thermal convection occurs as the fluid itself begins to move. Fluctuations then occur in the form of convective cells and become amplified as the temperature gradient increases. This continues until a critical value is reached at which point the system self- organizes into a pattern of hexagonally shaped cells, each cell made up of millions of individual water molecules.
Mathematically, it is possible to test the conditions necessary for such transitions to take place. This is done by testing the stability of the reference state to infinitesimal fluctuations by the formal procedure of linear stability analysis (Nicolis & Prigogine 1989, 1977). If the reference state is unstable to the fluctuations, there will be a qualitative change in the reference state beyond some critical threshold (or bifurcation point) of a control parameter. Self-organization occurs when this qualitative change in the reference state leads to new solutions that exist beyond the threshold of instability. In the above example of the Benard instability, self-organization occurs when the bifurcation parameter reaches a critical threshold value. At this point the system is no longer capable of damping the convective fluctuations, and the net result is a destabilization of the system. This destabilization leads to a qualitatively new state, namely, to the state which self-organizes into a hexagonally shaped pattern. In general, when bifurcations lead to new stable states, they are a source of newness in a system.
Similarly, if the brain becomes sensitive to small disturbances in the neuronal firing pattern of some brain cells, it may amplify such disturbances causing a bifurcation from its reference state. When this happens, more and more neurons are recruited into a homogeneous oscillation of increasing frequency and amplitude. The result is a traveling wave and an epileptic seizure (Kaczmarek & Babloyantz, 1977). This example is of particular relevance to our model of dreaming because of the many formal similarities between the REM sleep PGO wave and the epileptic spike and wave complex (Elazar & Hobson, 1985).
The phenomenon of self-organization is universal for all non-linear systems maintained far from equilibrium.
Levels of Self-Organization
Self-organization can be imagined to occur at several levels in the brain: at one level is the formation of relatively simple structures such as cortical columns or sets of columns in the visual cortex. These very simple structures give rise, cognitively, to fragments of images which occur in NREM sleep when cholinergic input from the brain stem is relatively low, but sufficient to maintain the brain far from equilibrium (which allows self-organization to take place). More complex image formation self-organizes when additional bifurcations occur due to a further increase in cholinergic input to the disinhibited forebrain.
When PGO burst neurons begin to fire, inducing phasic discharge in thalamic and cortical areas, even more complex image formation self-organizes as larger and larger areas of cortex are synchronously excited. Cognitively these bursts may lead to dream bizarreness for two reasons. First, the PGO waves induce neuronal patterns which are incongruous with but nonetheless integrated into the on going dream narrative. And second, the PGO waves, acting as environmental fluctuations, destabilize the existing neuronal organization causing a new neuronal pattern to self-organize whose cognitive correlate may be a narrative discontinuity such as the ". . child of perhaps 6 to 8 years, who later turned into Jason. . ." or "By this time Jason had vanished, and there seemed to be two adults with me. . ." These are examples of discontinuities whereby characters suddenly appear or change identity. Another type of discontinuity is illustrated by ". . we suddenly saw the Customs Bldg. . . ." in which the customs building suddenly appears in the narrative out of nowhere. Another type of discontinuity is illustrated by "We entered the building somehow. . ." The discontinuity illustrated by this excerpt is appearing inside the building without actually going through the steps necessary to get in.
At still a higher level, signals from the whole array of neuronal clusters comprising the rich cortical network, self-organize to produce dream narratives. For reasons that we will consider later, these narratives have a remarkable degree of stability. It interests us that this property could contribute to an overall coherence or "single mindedness" in dreams even in the presence of microscopic disorder. A schematic of the model is presented in Fig. 2.
In all cases, self-organization occurs because the neuronal system is non-linear and is maintained far from equilibrium. For example, at the level of a single neuron, the neuron is not in equilibrium because of the sodium and potassium gradients across its membrane (the concentration of sodium is higher outside the cell than inside and this difference is maintained by a sodium pump; the concentration of Potassium is higher inside than outside the cell).
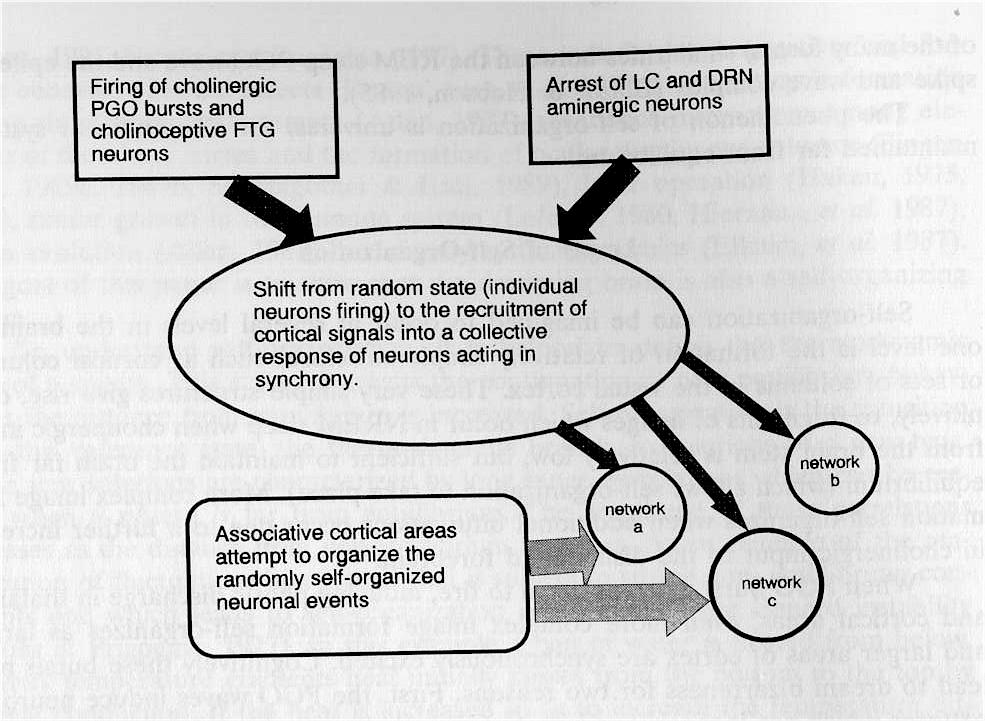
Fig. 2. Self-Organization Model of Neuronal Activity in Dreaming: Sketch of Self-Organization Model of Dreaming. An array of aminergically demodulated forebrain neurons receiving input from PGO and cholinergic brainstem neurons shift from individual activity into a collective response. This collective response is a result of the recruitment of cortical signals and the development of correlations among the neural processes leading to the emergence of self-organized properties such as the visual images of dreams. At the same time there is top down cortical activity which attempts to organize the randomly self-organized neuronal processes into a narrative. The attempts often lead to incongruities and discontinuities of narrative.
_______
It is, however, important to be aware of the level of description being used in the definition of a system. At a more macroscopic level of description, say a neural network, the interest shifts from whether a single neuron is in equilibrium to whether the network is in equilibrium. For example, the neural network consisting of forebrain structures will be driven far from equilibrium if bombarded by signals from the brain stem. The distance from equilibrium is least when there is only aminergic disinhibition and greatest when there is cholinergic input and PGO waves. In the former case, neuronal self-organization would not occur very readily and hence dreaming is relatively rare without cholinergic input. This is because the ability of a system to self-organize is proportional to its distance from equilibrium, which in turn is related to the constraints acting upon the system. While sleeping, external input is mostly absent so that only the internally generated input is able to maintain the brain-mind system far from equilibrium.
We may illustrate these different levels of self-organization schematically as follows:

Role of PGO Waves as Environmental Noise
We suggest that PGO waves appear to the cortical structures as environmental fluctuations. In this role the PGO waves act as a noisy bifurcation parameter and cause additional bifurcations which lead to additional self-organized images that add to the bizarreness of dream narratives. Since PGO waves occur predominantly during the REM state, it is not surprising that more vivid hallucinatory images would occur more frequently during the REM state than in the noise free NREM environment.
In REM where the environment is noisy due to bursts of PGO spikes, new mathematical solutions develop as a result of processes called probability amplitude peak splitting, and shifted transition points. These two processes have their cognitive correlates in the appearance of new images and in the appearance of displaced images, respectively. Dream narratives in REM thus contain more discontinuities, and more incongruities owing to the existence of these additional possible mathematical solutions brought about by the PGO noise.
Novelty in Dreams and Self-Organization
It is known that the dreamer often feels that the dream just happens, the dreamer exercising little control over his or her actions in the dream (Hartmann, 1973). This non-directed state is consistent with what exists in other self-organizing systems. Even though self-organizing systems have external parameters that constrain the choices open to the self-organizing system, nonetheless, the system itself "decides" which of the many possible behaviors it will adopt. The choice is made through the fluctuations present within the system which push it to one or another stable state.
In the dreaming brain, the constraining forces come from internal memories: enduring records of conflict, desire, or concern; and more transitory traces of recent input, the so-called day residue of Freud. But within these constraints, the fluctuations can lead to an extremely wide repertoire of possible combinations. There is thus a large chance for novelty and innovation in dreaming as fluctuations play with a seeming infinite supply of existing images and story lines.
MATHEMATICAL MODELING OF THE SELF-ORGANIZATION THEORY
The hypothesis of the previous section— that the disinhibited brain self-organizes to produce dreams—is schematically modeled in this section. Any tractable model of such a complex behavior as REM sleep/dreaming must greatly simplify that behavior. Our hope is to be able to capture the important dynamics of the system within a simplified model. We further hope to show that one or more of a class of equations describing the evolution of a variable is sufficiently universal that it can capture the qualitative behavior of self-organization in dreaming.
Our approach to modeling is based upon the evidence (Nicolis & Prigogine, 1989) that near a bifurcation point, a system may be described by equations which have the same form as the so-called bifurcation equations. Bifurcation equations describe the dynamics of a collective variable (also called an order parameter). Close to its bifurcation points, a system's equations are satisfied by the collective variables of the system. Thus, a complex system with many variables becomes mathematically tractable near its bifurcation points. With the use of bifurcation equations it becomes possible to think about mathematically modeling such a complex system as the dreaming brain. We shall take the collective variable or order parameter to be the dream image at one level of description; at a higher level of description the variable will include narrative plot formation (see discussion in the previous section on the different levels of self-organization during dreaming).
Verhulst Type Models
We now consider a class of models which describes the temporal evolution of dream image formation as a function of the relative firing rates of the Dorsal Raphe Nuclei (DRN), Locus Coeruleus (LC) complex and the Pontine Cholinergic nuclei (Quattrochi et al. 1989). This class of model is formally consonant with previous descriptions of population dynamics at the neuronal level used to model the periodic alternation of REM and non-REM sleep (McCarley & Hobson, 1975). At a very simple level, the model equation may be expressed as follows (also see, for example, Horsthemke & Lefever, 1984)
(1)
dx/dt = ax - xm, m $ 2
where the variable x which may be formally equated with the density of images in a dream report (the number of images divided by the word length of the report, for example) is the order parameter or collective variable of the system, As the pattern that ultimately develops from the many neuronal interactions, it is the variable that organizes "everything" (Haken, 1981). Practically, it allows us to describe the complicated dynamics of the brain mind system near its transition or bifurcation points. While always bearing in mind that the variable x is in fact such a deep variable, we shall henceforth speak of it heuristically as expressing the occurrence of a dream image, or the occurrence of dreaming, depending upon the level of description.
The parameter a which is the assumed bifurcation parameter expresses the difference between normalized firing rates of the DRN/LC complex and the Pontine cholinergic complex. Incidentally, it would also be possible to use serotonin (5HT) and norepinephrine (NE) concentrations in lieu of the DRN/LC firing rate, and acetylcholine (Ach) concentration in lieu of cholinergic firing rates as measures for the parameter a. This is because both neurotransmitter release and concentration appear to be linear functions of aminergic neuronal discharge rates in waking and sleep. In the case of m = 2, Equation (1) is the well known Verhulst equation for the evolution of a population, though it has found application to many other phenomena. In the Verhulst equation, a expresses the difference between the birth and death rates of the population. The second term accounts for the finite resources available to a population by restricting its growth. In our application to the brain, a expresses the difference between the firing rates of two brain stem neurotransmitter systems, aminergic and cholinergic.
We will begin with this very simple Verhulst equation, and show that it can be used to highlight some of the basic notions involving self-organization in dreaming introduced in previous sections. The equation is
(2)
dx/dt = ax - x2
The solution of this equation is:
(3)
x(t) = x(0) eat {1 + x(0) [(eat-1)/a]}-1
Stationary solutions are obtained by putting dx/dt = 0. One stationary solution is x = 0 which is a stable solution so long as a is negative. In terms of population dynamics, when the death rate exceeds the birth rate (a negative), the solution x = 0 simply means that the population has ceased to exist. When the birth rate is equal to the death rate (a = 0), the zero population solution becomes mathematically unstable as may be verified from a linear stability analysis as shown in Nicolis & Prigogine (1989). This mathematical instability is equivalent to the solution x = 0 being physically untenable. When the birth rate exceeds the death rate (a > 0), the population takes on finite values. The point a = 0 is a bifurcation point since a new branch of stable stationary states x = a appears for a > 0. That is, there is a qualitative change in the solution x at a = 0 (see Fig. 3).
Interpreting these results in terms of dreaming, the a > 0 solution corresponds to the sudden appearance of a dream image, for example the appearance of the customs house " . . . we suddenly saw the customs building. . ." in the customs house dream.
This simple model which is controlled by the single parameter a is already able to describe an important mechanism leading to a qualitative change of behavior beyond the threshold of instability. This is the phenomenon of bifurcation. Assuming that such a mechanism occurs during dream onset, the model is a useful way of illustrating the dependence of dream onset on the control parameter a. The model predicts that dream images do not form until a critical level of cholinergic neurotransmitters relative to DRN/LC neurotransmitters is attained. Note that according to this model PGO waves are not necessary for dream image formation. All that is needed is a sufficiently large difference between aminergic and cholinergic input to the forebrain.
We now formally introduce PGO bursts (whose frequency is assumed to be rapid compared with the macroscopic time scale of the dream) into the Verhulst model as environmental fluctuations. If the system is coupled to a fluctuating environment the parameters become stochastic quantities. We first assume that the PGO bursts can be modeled as white noise so that we may decompose the parameter a into a fluctuating and non-fluctuating part by assuming at is given by a stationary process as follows:
(4)
at = a + F gt
where a is its average value, gt is Gaussian white noise and F is the variance which measures the intensity of the PGO waves. Thus, a now becomes a stochastic parameter composed of its average value a plus a fluctuating part given by F gt. For example, the difference between the concentrations between the two brain stem neurotransmitter systems is now no longer assumed to be unaffected by other events in its surroundings, such as PGO bursts. a is now taken as the average value of this difference, but is assumed to also contain a fluctuating part which we identify as bursts of PGO waves.
Equation (2) is now replaced by a stochastic differential equation (see Horsthemke & Lefever, 1984, or Kahn, et al. 1985 for details of the procedure) to yield,
(5)
dxt = (axt - xt 2 )dt + F xt dWt
where xt is the stochastic variable and Wt is the Wiener process (that is, it is the basic stochastic process of Brownian motion).

Fig. 3. Verhulst Model of Dream Onset. Bifurcation diagram of the stationary states of x for the Verhulst model. The parameter a expresses the difference in normalized firing rates of the DRN/LC and Cholinergic nuclei. For a < 0 the state x = 0 is a stable stationary state (bold line). For a > 0 the state x = 0 becomes unstable (dashed line), but a new state x = a appears which is stable. The figure shows that the state in which the dreams occur, x > 0, does not appear until cholinergic input exceeds the aminergic input (a > 0)
_______
When this equation is solved for the extrema of the probability distribution of x (equivalent to its solutions) two transition points, one at a = 0 as before in the noise-free case without PGO waves, and the other at a =F2 /2 are found to exist. In the absence of PGO bursts, only one transition or bifurcation point (at a = 0) existed. The PGO-induced point at a = F2/2 corresponds to a qualitative change in the dream image variable, x. For example, in a dream report this would correspond to the appearance of a new image [e.g., in the Customs House dream: "In each of two other rooms was a girl (young lady) in nurse's uniform"]. The narrative both accommodates the new image and is influenced by it. This second PGO-induced transition point occurs as a result of the non-linearity of the system. Thus, the effect of PGO waves has been to alter the form of x, our dream occurrence variable, by splitting the transition point into two, and by shifting the original transition point from a = 0 to a = F 2/2.
The above results are quite general for models of the Verhulst type, for if we replace the power 2 in Equation (5) by an arbitrary power in we find that all these models still contain two transition points, one at a = 0, and the other at a = F 2 /2 ( (Horsthemke & Lefever, 1984). While this effect illustrates how bursts can alter the formation of dreams, it predicts only one additional transition in the presence of PGO waves. This additional transition occurs when higher values of a are reached, that is, when larger differences between cholinergic and aminergic firing rates exist.
It is possible that PGO waves cannot be adequately modeled as white noise. White noise contains all frequencies with infinitely short correlation times, and it may be that PGO waves are better modeled as units with specific frequencies that occur at definite, but unpredictable intervals of time. There is evidence that this is the case, since PGO waves have features of unitary all-or-nothing processes (Callaway, et al. 1988). Such a process is called dichotomous Markov noise.
When the occurrence of dreaming with PGO bursts is modeled as dichotomous Markov noise (instead of white noise) a rich set of transitions is observed that more accurately reflects the dreaming state. Multiple transitions means that instead of a relative continuity in dream narrative, different images compete for expression with the result that narrative discontinuities often appear. Such multiple transitions are shown schematically in Figs. 4 and 5 where instead of one story line continuing as the only stable state (represented by the single humped distribution of the variable x), two or more nearly equally probable images appear, represented by the double humped distribution in the second of Figs. 4a, and by the multiple distributions in Fig. 4b.
The significance of multi-modal distributions, each of which represents the probability that x will occur, is that any one of the images may form since the system is multi-stable. Which image is actually self-organized depends upon the "holding power" of the existing narrative (this is mathematically modeled as a hysteresis effect), and how internal perturbations (or external if they can get through) "select" one or another of the potential states to self-organize. This is exemplified in the Customs House dream passage ". . . a child of perhaps 6 to 8 years, who later turned into Jason but who, at first, seemed like a stranger." Here, either of the two images, that of the stranger which appeared first, or that of the author's nephew Jason which appeared second, could persist. In the example cited, the image of Jason replaced that of the stranger.
Figure 4c sketches a typical bifurcation diagram illustrating how the collective variable x may undergo bifurcations as the parameter a increases. For example, a dream which may have few images when the neurotransmitter differences are small, will bifurcate into multiple images as the differences widen (either further demodulation or increased cholinergic activation), For example, in the customs house dream the image of a cradle-like bed with a nurse and a baby is quickly followed by an image of a room with young children with ancient faces and then quickly to an image of a room with a judge and the dreamer's two sisters.
In Fig. 4d we have sketched the case when PGO bursts exist. The probability density is plotted against x. This figure is to be compared to the first of Figs. 4a. When F 2 > F 2c (PGO intensity greater than some critical value) this most probable image of Fig. 4a has now become the least probable and, in fact, is replaced by two different (equally probable) images. One is eventually chosen. An example of this bimodal state might entail an initial uncertainty in who or what the dreamer sees. This occurs in the custom house dream in the previously cited passage when the dreamer sees a young boy who he believes later to be his nephew Jason, ". . . a child of perhaps 6 to 8 years, who later turned into Jason but who, at first, seemed like a stranger."
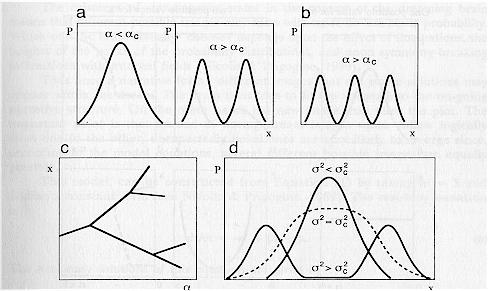
Fig. 4. Effects of PGO Bursts and Increasing Cholinergic, Decreasing Aminergic Input on the Occurrence of Dream Images. Sketches of the Probability P(x) that x will take on specific values for given values of a. The parameter a represents, as before, a measure of the difference between cholinergic and aminergic input to forebrain structures. In 4a we see that an initially uni-modal distribution predicting one value for the variable x becomes bi-modal when a becomes greater than some critical value a,. Figure 4b shows many such nearly equal probable values for x. A bifurcation tree representing the situation in 4b is sketched in 4c. Figure 4d shows how an initially single humped distribution becomes multi-valued as the intensity of environmental noise increases (based on the so-called genetic model reported in Horsthemke & Lefever (1984)). Noise intensity is measured by values of F 2.
Figure 5 further illustrates the occurrence of multiple values of x. The figure shows that by increasing the amplitude of the noise the system undergoes a series of transitions not present when noise is absent. The figure depicts the case when fluctuations are modeled as dichotomous instead of white noise as analyzed in Horsthemke & Lefever (1984).
The figure compares the noise free environment with that when noise is present. Noise introduces multiple values of x. In a dream these added transitions reflect new dream imagery and are hypothesized to at least partially account for dream discontinuities and incongruities of dreaming such as the sudden appearance of characters, objects, or places in a dream. For example, the sudden appearance of ". . . we suddenly saw the customs bldg. . .," or the incongruous images, ". . . a large cradle-like bed in which were a fully dressed nurse and a baby."
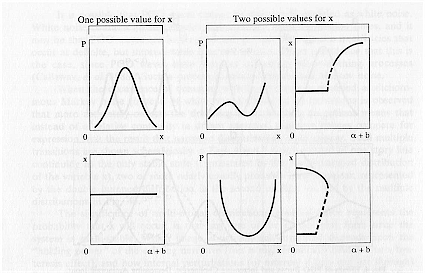
Fig. 5. Effects of PGO Bursts on the Occurrence of Dream Images: Dichotomous Noise Model. Phase and corresponding bifurcation diagrams for the steady state behavior of the Verhulst model as a function of PGO waves modeled as dichotomous noise based on analysis of the Verhulst equations in Horsthemke & Lefever (1984), and Horsthemke (1980). P(x) is the probability that x will occur, where x is equated with the ability to form dreams. The bifurcation parameter is a, and the amplitude of the noise is given by b in the figure. Noise introduces multiple values of x, that is, added transitions occur when the PGO waves impinge upon the brain. These added transitions reflect new dream imagery and are hypothesized to, at least partially, account for dream discontinuities and incongruities of REM dreaming.
Other Models
In addition to the Verhulst class of equations, it is possible to identify another class of simple mathematical models which reproduce features of self-organization identified in the previous section but which are not adequately modeled by the Verhulst equation. One such model shows the existence of simultaneous multiple stable stationary states. This is an important feature to utilize in constructing a theory of dreaming because it guarantees both pluripotentiality and unpredictability.
The existence of simultaneous states in the context of the dreaming brain means that different possible images may form with more or less equal probability. Which one the brain actually "chooses" depends upon the effect of fluctuations, the heights of the peaks of the probability distributions, and upon symmetry-breaking interactions with external fields (Nicolis & Prigogine, 1989).
Thus once a narrative forms, different images that are stable solutions may appear within the dream. The brain then tries to fit the images into the on-going narrative structure. On the other hand, the new image may alter the plot. The important point is that instead of having dream images which follow logically from one to the other, unexpectedly novel ones are very likely to emerge since, according to the model equations, several different possible images are equally possible.
This model, can be constructed from Equation (1) by taking m = 3 and adding a constant term (see Nicolis & Prigogine, 1989). The resulting equation is
(6)
dx/dt = -x 3 + $ x + m .
The stationary solutions of this equation are given by
(7)
-x 3 + b x + m = 0.
Here the order parameter x evolves according to a third order non-linear equation. We heuristically identify x (as before) with the formation of dream images, or narratives (though, as previously discussed, x may be defined quantitatively as the density of images in a dream report). We take the parameter m to be the ratio of cholinergic to aminergic input. The parameter b is interpreted as a measure of the level of activation of the brain (as measured, for example by EEG recordings). This is further elaborated upon when we discuss Fig. 6b.
The stationary state solutions of (7) are depicted in Fig. 6a for a fixed level of b and in Fig. 6b for a fixed value of m .
In region 1 of Fig. 6a the ratio of cholinergic to aminergic input is small, and the probability of image formation is low, but finite. We identify region 1 with NREM sleep. In region 2 the probability of having dream imagery increases, but is still low, remaining on branch a. However, once the cholinergic to aminergic ratio reaches a threshold value m 2, presumably such that REM is triggered, the probability that dream images will self-organize jumps dramatically, moving from branch a to branch b. There is some support for this phenomenon in the experimentally confirmed exponential rise in neuronal excitability of REM onset predicted by the Volterra-Lotka model (McCarley & Hobson, 1975).
Coming down from a REM state on branch b in region 3, dreaming should persist even if the cholinergic to aminergic ratio decreases below m 2. Not until it falls below m 1 will the probability fall to values depicted on branch a. This is an example of hysteresis. In region 2 the system has bistability, the system may be either in a REM or in a NREM state depending upon the system's history. If it is
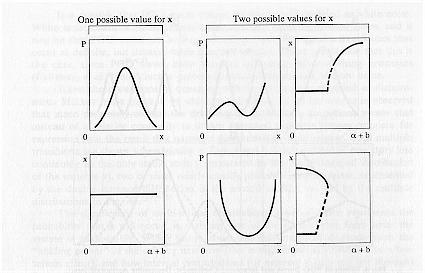
Fig. 6. Neuromodularity and Activation Influences on REM and NREM Sleep Stages. Sketch of the bifurcation diagram for the model given by equation (7) showing its stationary solutions. In 6a the effect of the cholinergic to aminergic ratio, parameter :, on dream formation is shown at a constant level of brain activation, $ = a constant. In 6b the effect of the electrical energy activation parameter, $ is shown for a given level of the cholinergic to aminergic ratio, : = a constant. The sketch is adapted from Nicolis & Prigogine (1989) who discuss the bifurcation properties of dissipative systems described by equations (6) and (7).
in a REM state it tends to remain there until the firing rate decreases to m 1. If it is in NREM it tends to remain there until the firing rate increases to m 2. To our knowledge this hysteresis effect has not yet been found (or looked for) experimentally. This hysteresis effect exemplifies one of the greatest virtues of modeling: its ability to suggest new questions and new modes of inquiry.
The theory also predicts the existence of bimodal distributions for the cognitive variables, e.g., visual intensity, vividness, sense of movement, bizarreness, etc. One kind of bimodal distribution is simply the occurrence of multiple values taken on by the variables depending upon whether one is in the REM or NREM stage. The other, more interesting kind of bimodality is that depicted in Fig. 4 in which the REM state itself yields multiply stable states. For example, visual intensity, would be bimodally distributed in REM; the chosen intensity would depend upon the result of the bifurcation (see, for example, Fig. 4c). This behavior of the model thus suggests still another possible hypothesis: that visual image intensity will be experienced at two levels and not along a continuum.
Continuing with examination of Fig. 6, Fig. 6b shows how dream image formation is affected by increasing values of activation level for a given value of the cholinergic to aminergic ratio. Here, where dream image formation x is plotted against brain activation, b , for fixed cholinergic to aminergic input, m , we find two branches that can simultaneously exist beyond a critical value b c, When on the top or sleep branch, dream images increase with increasing brain activation; the brain state changes from NREM to REM in agreement with the observation that REM sleep onset is accompanied by an increase from low brain activation to high brain activation. When on the lower or waking branch, the opposite is true, dream images decrease with increasing activation, also in agreement with observation that there is a high level of brain activation during waking. If we follow the waking branch from the right (from high activation levels) to the left (toward lower activation levels) a point is reached at which the activation level b drops to a sufficiently low value b c, at which NREM sleep is kicked in (a transition to the sleep branch takes place). The observed occurrence of dream like mentation at sleep onset is consistent with this increase in the dream image variable x.
We note that during the night, unless one is awakened, the sleeper remains on the upper branch going from NREM to REM and back again in cyclical fashion, in qualitative agreement with the observed NREM/REM sleep cycle. Prior to early morning awakening there is a transition to the lower "waking" branch. The processes leading to this break in the NREM-REM cycle undoubtedly include the effects of increasing body temperature and the state of the circadian clock as well as changes in the brain stem modulatory systems themselves. Further consideration of these effects are beyond the scope of this paper. For heuristic purposes we also ignore here the important impact upon the system of the ratio between external inputs (or their internal representations) and the internally generated PGO signals. The relationship between this factor (I) the activation level (A) and the neuromodulatory ratio (M) has been discussed and modeled in a recent paper (Hobson, 1990b).
POSSIBILITIES FOR EXPERIMENTAL VERIFICATION
Just as we can construct new paradigms for human psychophysiology, it may be possible to look for the theoretically predicted bifurcation parameter, its threshold value, and a hysteresis effect in experimental animal models. We would be looking for the value of the cholinergic to aminergic ratio : when the first REM period began. If REM develops slowly as : gradually increases we can conclude that the cholinergic to aminergic ratio is not the bifurcation parameter. On the other hand if an all or nothing effect is observed whereby the REM state is abruptly triggered when : reaches a critical value we may conclude that when : reaches that critical value, a bifurcation has occurred. Further, if hysteresis exists, this REM period would persist until the cholinergic to aminergic ratio reached m = m l, representing a value of : which is less than that needed to initiate the REM period. It may be possible to measure : with a suitably outfitted cat which allowed measurement of the relative values of the neurotransmitters Ach, and NE and 5HT. Such studies are now feasible using microdialysis technology (Lydic et al. 1991).
Alternatively, it is possible to administer carbachol a cholinergic agonist and determine what dosage is required to produce REM in a given amount of time. Assuming that the aminergic system does not change upon administration of carbachol, we could obtain the value of m needed to change the cat's state to REM. Once the cat was in REM an aminergic agonist could be administered to see what dosage is needed to bring it's state out of REM. Assuming that the cholinergic system does not change upon administration of the aminergic agonist, this would provide the value of : needed to bring the cat out of REM. If hysteresis were present, the value of : needed to push the cat into REM sleep would be greater than that needed to pull the cat out of that state.
SELF-ORGANIZATION THEORY OF
DREAMING AND WAKING
In Erdi & Barna (1987) self-organization and noise-induced transitions were used to model the formation of ocular dominance columns. Noise-induced transitions were also used to study retinotopic connections (Erdi & Barna, 1984). The authors stated that retinotectal connections and ocular dominance columns might be generated by "noise-induced self-organizing mechanisms." Their 1984 model predicted that ordered connections become established only in the presence of noise. This unusual result, in fact, was initially predicted by Lefever (Horsthemke & Lefever, 1984) in Lefever's so-called genetic model.
The implications of this insight are profound. Order out of randomness is seen to be not only possible but in some cases necessary, that is, noise (randomness, or chaos) is sometimes necessary to trigger the emergence of organization. With respect to acceptance of the activation-synthesis theory of dreams, an appreciation of this dialectic between chaos and order might go a long way to easing the qualms of critics who have imagined an unintended and undesirable return to a 19th century pre-Freudian nonsense theory of dreaming.
The fundamental role of self-organization is also brought out by Szentagothai and Erdi (Szentagothai & Erdi, 1989). As in our theory, they recognize that noise plays a crucial role in transition phenomena. They found that "no sensory input is needed . . . for orderly function. Lacking sensory input the activity has, obviously, to originate from the known spontaneous activity of neurons. Neurons become spontaneously active . . ." (ibid., p. 374). This finding that sensory input is not necessary for orderly neuronal functioning supports the concept that self-organization occurs in dreaming where sensory input is lacking. In fact, these authors point out "Since spontaneous activity of neurons is usually random, an organized activity can emerge only by self-organization of random neural noise. . ." (ibid., p. 374). Recently, the neurobiologist Rodolfo Llinas has also suggested just such a concept to help explain dreaming (Llinas & Pare, 1991).
SUMMARY AND CONCLUSIONS
The hypothesis of this paper is that during REM sleep the random neuronal discharges of the aminergically demodulated and cholinergically activated brain become correlated by the mechanism of self-organization. This hypothesis accounts for the appearance of dream images and for the observation that the images often do not appear in logical sequence as they might if a fully cognitive top down plan were being implemented. Images are individually self-organized in dreaming sleep. Bizarreness in dreams occurs when these newly self-organized images are incongruously incorporated into an on-going dream, and when the PGO noise-induced bifurcations directly affect a neuronal pattern (whose cognitive correlate is an image) that is already a part of an on-going dream. In this case the dreamer may experience not only an incongruous juxtaposition of new images, but a bizarre change to an on-going image leading to a hallucinatory and disorienting dream experience. Mathematically, this happens because the noise (PGO wave) induces an additional solution to bifurcate from an existing one.
In order for neuronal activity to self-organize as we have hypothesized, neuronal activity must be maintained far from equilibrium. We have taken the self-organization bifurcation parameter to be the ratio of cholinergic to aminergic input to the brain. This ratio reflects how far the system is from equilibrium. The theory predicts that when this ratio reaches a critical threshold, existing neuronal activity patterns destabilize and self-organize to new ones, whose cognitive correlates are dream images. We have further hypothesized that PGO waves act as a noisy self-organization bifurcation parameter. As such the PGOs cause existing neuronal patterns to bifurcate into new patterns characterized by long range correlations whose cognitive correlates are dream images.
Finally, we were able to mathematically model the dynamics of the dreaming brain because a self-organizing system contains an order parameter which is the collective variable satisfied by the system equations. The existence of this order parameter greatly simplifies the dynamics of a self-organizing system near its bifurcation points because the system is constrained to just a few behaviors there. The equations can, therefore, be cast in a universal normal form. The question then becomes how to identify the bifurcation parameters that structure the system when their critical values are reached. For dreaming the ratio of cholinergic to aminergic neurotransmitter concentration was hypothesized to be a bifurcation parameter. At a critical value of this ratio dreaming begins. This hypothesis as well as the possible existence of other bifurcation parameters as an electrical activation level must be experimentally tested to validate the theory.
ACKNOWLEDGMENTS
This paper was supported by NIH grant NIH, 13.923 and the MacArthur Foundation Mind-Body Network. We gratefully acknowledge R. Stickgold, J. Sutton, E. Schott-Pace and C. Rittenhouse for comments on a draft of this article.
REFERENCES
Aghajanian, G. K, & Van der Maelen, C. P. (1986). Specific systems of the reticular core: Serotonin. In V. B. Mountcastle (ed), Handbook of Physiology—The Nervous System, volume IV, section 1. Bethesda: American Physiological Society, 237-256.
Allen, P. M. (1982), Self-Organization in the urban system in Self-Organization and Dissipative Structures, W. C. Schieve and P. M. Allen (eds.), University of Texas Press, Austin, pp. 132-158.
Antrobus, J. (1991). Dreaming: cognitive processes during cortical activation and high afferent thresholds. Psychological Review, 98, 96-121.
Atlan, H. (1989). Automata network theories in immunology: their utility and their under determination. Bulletin of Mathematical Biology, 51, 247-253.
Atlan, H. (1987). Self Creation of Meaning. Physica Scripta, 35.
Babloyantz, A., Salazar, J. M., & Nicolis, C. (1985). Evidence of chaotic dynamics of brain activity during the sleep cycle. Physics Letters, 111A, 152-156.
Bonato, R. A., Moffitt, A. R., Hoffmann, R. F., Cuddy, M. A., & Wimmer, F. L. (1991). Bizarreness in dreams and nightmares, Dreaming, 11, 53-62.
Callaway, C. W., Lydic, R., Baghdoyan, H. A., & Hobson, J. A. (1988). Pontogeniculoocipital waves: Spontaneous visual system activity during rapid eye movement sleep. Cellular and Molecular Neurobiology.
Clark, J. W., Rafelski, J., & Winston, J. V. (1985). Brain without mind: computer simulation of neural networks with modifiable neuronal interactions. Physics Reports, 123, 215-273.
Deneubourg, J. L., Goss, S., Pasteels, J. M. Fresneau, D., & Lachaud, J. P. (1987a). Self-organization mechanisms in ant societies (II): Learning in foraging and division of labor in From Individual to Collective Behavior in Social Insects, J. M. Pasteels and J. L. Deneubourg (eds.), Birkhausser Verlag, Basel, Boston, pp 177-196.
Deneubourg, J. L., Aron, S., Goss, S., & Pasteels, J. M. (1987b). Error, communication and learning in ant societies, European Journal of Operational Research, 30, 168-172.
Edelman, G. (1990). The Remembered Present: A Biological Theory of Consciousness.
Elazar, Z., & Hobson, J. A. (1985). Neuronal excitability control in health and disease: A neurophysiological comparison of REM sleep and epilepsy. Progress in Neurobiology, 25, 141-188.
Elkaim, M., Goldbeter, A., & Goldbeter-Merinfeld, E. (1987). Analysis of the dynamics of a family system in terms of bifurcations, J. Social Biol. Struct., 10, 21-36.
Erdi, P., & Barna, G. (1987). Self-Organization in nervous systems: some illustrations. In Lecture Notes in Biomathematics, 71, Mathematical Topics in Population Biology, Morphogenesis and Neurosciences (Eds.), E. Teramoto & M. Yamaguti. Springer-Verlag, Berlin.
Erdi, P., & Barna, G. (1984). Self-organizing mechanism for the formation of ordered neural mappings. Biol. Cybern., 51, 93-101.
Flicker, C., McCarley, R. W., & Hobson, J. A. (1981). Aminergic neurons: State control and plasticity in three model systems. Cellular and Molecular Neurobiology, 1, 123-166.
Globus, G. G. (1989). Connectionism and the dreaming mind. The Journal of Mind and Behavior, 10, 179-196.
Gray, C. M., Konig, P., Engel, A. K,, & Singer, W. (1989). Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature, 338, 334-337.
Haken, H. (1981) The Science of Structure: Synergetics, Van Nostrand Reinhold Company.
Haken, H. (1975). Reviews of Modem Physics, 47, 67-121.
Hartmann, E. (1973). The function of sleep, New Haven, Yale University Press.
Hiernaux, J. R., Lefever, R., Uyttenhove, C., & Boon, T. (1987). Tumor dormancy as a result of simple competition between tumor cells and cytolytic effector cells in Paradoxes in Immunology, G. W. Hoffmann, J. G. Levy, and G. T. Nepom (eds.), CRC Press, Inc., Boca Raton, Florida, pp. 95-109.
Hobson, J. A. (1990a). Sleep and Dreaming. Neuroscience, February, 10(2), 371-382.
Hobson, J. A. (1990b). A.I.M.: Activation, input source and modulation, a neurocognitive model of brain-mind state. Presented at the Arizona Conference on Sleep and Cognition, January 1989, American Psychological Association.
Hobson, J. A. (1989). Sleep. W. H. Freeman and Company, New York.
Hobson, J. A. (1988). The Dreaming Brain, Basic Books, Inc., New York.
Hobson, J. A., & Schmajuk, N. A. (1988). Brain state and plasticity: an integration of the reciprocal interaction model of sleep cycle oscillation with attentional models of hippocampal function. Archives Italiennes de Bioiogie, 126, 209-224.
Hobson, J. A., Hoffman, S. A., Helfand, R., & Kostner, D. (1987). Dream bizarreness and the activation-synthesis hypothesis. Human Neurobiology, 6, 157-164.
Hobson, J. A., & Steriade, M. (1986). Neuronal basis of behavioral state control. In Handbook of Physiology: The Nervous System, IV, V. Mountcastle and F. E. Bloom (eds.), 701-823.
Hobson, J. A., & McCarley, R. W. (1977). The brain as a dream-state generator: An activation-synthesis hypothesis of the dream process. American Journal of Psychology, 134, 1335-1368.
Horsthemke, W., & Lefever, R. (1984). Noise-induced transitions. Springer-Verlag, Berlin.
Horsthemke, W., & Lefever, R. (1981). Voltage-noise induced transitions in electrically excitable membranes. Bioph. J., 35, 415-423.
Horsthemke, W. (1980). Non-equilibrium transitions induced by external white and coloured noise, in Dynamics of Synergistic Systems, Springer Series Synergetics, vol. 6, ed. by H. Haken, Springer, Berlin.
Kaczmarek, L. K. Babloyantz, A. (1977). Spatiotemporal patterns in epileptic seizures. Biological Cybernetics, 26, 199-208.
Kahn, D., & Hobson, J. A. (1991a). Self-organization theory of dreaming. Sleep Research, 20, 141.
Kahn, D., & Hobson, J. A. (1991b). Pontogeniculoocipital (PGO) waves produce noise-induced transitions in REM sleep. Sleep Research, 20, 142.
Kahn, D., De Palma, A., & Deneubourg, J. L. (1985). Noisy demand and mode choice. Transportation Research, 19, 143-153.
Keeler, J. D., Pichler, E. E., & Ross, J. (1989). Noise in neural networks: thresholds, hysteresis, and neuromodulation of signal-to-noise. Proc. Natl. Acad. Sci. USA, 86, 1712-1716.
Lefever, R. (1980). Dynamics of cell-mediated immune response, in Dynamics of Synergistics Systems, Springer Series Synergetics, vol. 6, ed. by H. Haken, Springer, Berlin.
Llinas, R. R., & Pare, D. (1991). Of dreaming and wakefulness. Neuroscience, 44, 521-535.
Lydic, R., Baghdoyan, H. A., & Lorinc Z. (1991). Microdialysis of cat pons reveals enhanced acetylcholine release during state dependent respiratory depression. Am J Physiol, 261, 766-770.
McCarley, R, W. and Hoffman, E. (1981). REM sleep dreams and the activation-synthesis hypothesis. Am. J. Psychiatry, 138, 7.
McCarley, R. W., & Hobson, J. A. (1975). Neuronal excitability modulation over the sleep cycle: a structural and mathematical model. Science, 189, 58-60.
Mamelak, A. N., & Hobson, J. A. (1989a). "Nightcap: a home-based sleep monitoring system." Sleep, 12 157-166.
Mamelak, A. N., & Hobson, J. A. (1989b). Dream bizarreness as the cognitive correlate of altered neuronal behavior in REM sleep. Journal of Cognitive Neuroscience, 1, 201-222.
Merritt, J. M., Stickgold, R., Pace-Schott, E., Williams, J., & Hobson, J. A. (1993). "Emotion profiles in the dreams of young adult men and women." Consciousness and Cognition, Submitted.
Moffitt, A., Hoffmann, R., Wells, K., Armitage, R., Pigeau, R., & Shearer, J. (1982). Individual differences among pre- and post-awakening EEG correlates of dream reports from different stages of sleep. Psychiatric Journal of the University of Ottawa, 7, 111-125.
Nicolis, G., & Prigogine, I. (1989). Exploring Complexity, W. H. Freeman and Company, New York.
Nicolis, G., & Prigogine, I. (1977). Self-Organization in Non-equilibrium Systems. John Wiley, New York.
Porte, H., & Hobson, J. A. (1993). "Fictive motion in REM sleep: A testing ground for dream theory." In preparation.
Posner, M. I. (1989). Foundations of Cognitive Science, MIT Press, Cambridge, MA.
Quattrochi, J. J., Mamelak, A. N., Madison, R. D., Macklis, J. D., & Hobson, J. A. (1989). Mapping neuronal inputs to REM sleep induction sites with carbachol-fluorescent microspheres. Science, 245, 984-986.
Resnick, J., Stickgold, R., Rittenhouse, C., & Hobson, J. A. (1993). "Self-representation and bizarreness in the dreams of young children. Consciousness and Cognition, Submitted.
Rittenhouse, C., Stickgold, R., & Hobson, J. A. (1993). "Global constraints on discontinuities in dreams." Consciousness and Cognition, Submitted.
Rittenhouse, C., Stickgold, R., Hobson, J. A. (1991). "Dream discontinuity: insertion, transformation, and removal." Sleep Research, 20.
Sakai, K., Salvert, D., Touret, M., & Jouvet, M. (1977). Afferent connections of the nucleus raphe dorsalis in the cats as visualized by the horseradish peroxidase technique. Brain Research, 137, 11-35.
Sartre, J. P. (1980). The Psychology of Imagination, Citadel Press, Secaucus, NJ.
Servan-Schreibe, D., Printz, H., & Cohen, J. D. (1990). A network model of catecholamine effects gain, signal-to-noise-ratio, and behavior. Science, 249, 892-895.
Singer, W. (1989a). Search for coherence: a basic principle of cortical self-organization. Concepts in Neuroscience, 1, 1-11.
Singer, W. (1989b). The role of acetylcholine in use-dependent plasticity of the visual cortex, In Brain Cholinergic Systems (eds.), M. Steriade & D. Biesold. Oxford University Press, Oxford.
Singer, W. (1988). Self-organization of cognitive structures. Proceedings of the Pontifical Academy of Sciences, Vatican City, October 19-24.
Stickgold, R., Rittenhouse, C., & Hobson, J. A. (1993b). "Dream splicing: A new technique for assessing thematic coherence in subjective reports of mental activity." Consciousness and Cognition, Submitted.
Stickgold, R., Pace-Schott, E., & Hobson, J. A. (1993a). "A new paradigm for dream research: Mentation reports following spontaneous arousal from REM and NREM sleep recorded in a home setting." Consciousness and Cognition, Submitted.
Stickgold, R., Rittenhouse, C., & Hobson, J. A. (1991). "Dream coherence: Is beauty in the eye of the beholder?" Sleep Research, 20.
Sutton, J., Rittenhouse, C., Pace-Schott, E., Stickgold, R., & Hobson, J. A. (1993). "Graphing and Discontinuity in Narrative Reports. Consciousness and Cognition, Submitted.
Sutton, J., Mamelak, A., & Hobson, J. A. (1992). Modeling states of waking and sleeping. Psychiatric Annals, 22, 3.
Sutton, J., Mamelak, A., & Hobson, J. A. (1991). "Neural network model of state-dependent sequencing." Sleep Research, 20.
Sutton, J. P., Beis, J. S., & Trainor, L. E. H. (1988). A hierarchical model of neocortical synaptic organization. Mathl. Comput. Modeling, 11, 346-350.
Szentagothai, J., & Erdi, P. (1989). Self-organization in the nervous system. J. Social Biol. Struct.,
12, 367-384.Williams, J., Merritt, J., Rittenhouse, C., & Hobson, J. A. (1991, in press). Bizarreness in dreams and fantasies: Implications for the activation-synthesis hypothesis. Consciousness and Cognition.
Williams, J., Merritt, J., Rittenhouse, C., & Hobson, J. A. (1990). Bizarreness in dreams and fantasies: Implications for the activation-synthesis hypothesis. Sleep Research, 19, 142.
Laboratory of Neurophysiology, Department of Psychiatry, Harvard Medical School, Boston, Massachusetts 02115. 2Requests for reprints should be sent to J. A. Hobson, Laboratory of Neurophysiology, Department of Psychiatry, Harvard Medical School, 74 Fenwood Road, Boston, MA 02115.